Зміст

• Крок

Тригонометричне рівняння - це рівняння з однією або кількома тригонометричними функціями змінної тригонометричної кривої x. Вирішення для x означає пошук значень тригонометричних кривих, тригонометричні функції яких обумовлюють істинність тригонометричного рівняння.

• Відповіді або значення кривих розв’язання виражаються в градусах або радіанах. Приклади:

x = Pi / 3; x = 5Pi / 6; x = 3Pi / 2; х = 45 градусів; х = 37,12 градуса; х = 178,37 градусів

• Примітка: На одиничному колі тригонометричні функції будь-якої кривої дорівнюють тригонометричним функціям відповідного кута. Одиничне коло визначає всі тригонометричні функції змінної кривої x. Він також використовується як доказ при вирішенні основних тригонометричних рівнянь та нерівностей.
• Приклади тригонометричних рівнянь:
  • гріх х + гріх 2х = 1/2; загар х + ліжечко х = 1,732;
  • cos 3x + sin 2x = cos x; 2sin 2x + cos x = 1.

1. Одиничне коло.
   • Це коло з радіусом = 1, де О - початок. Одиничне коло визначає 4 основні тригонометричні функції змінної кривої x, яка обводить її проти годинникової стрілки.
   • Коли крива зі значенням х змінюється на одиничному колі, тоді виконується:
   • Горизонтальна вісь OAx визначає тригонометричну функцію f (x) = cos x.
   • Вертикальна вісь OBy визначає тригонометричну функцію f (x) = sin x.
   • Вертикальна вісь AT визначає тригонометричну функцію f (x) = tan x.
   • Горизонтальна вісь BU визначає тригонометричну функцію f (x) = cot x.

• Одиничне коло також використовується для розв’язання основних тригонометричних рівнянь та стандартних тригонометричних нерівностей, враховуючи різні положення кривої х на колі.

Крок

1. Зрозумійте спосіб рішення.
   • Для розв’язання тригонометричного рівняння ви перетворюєте його в одне або кілька основних тригонометричних рівнянь. Розв’язування тригонометричних рівнянь зрештою призводить до вирішення 4 основних тригонометричних рівнянь.
2. Знати, як розв’язувати основні тригонометричні рівняння.
   • Існує 4 основних тригонометричних рівняння:
   • sin x = a; cos x = a
   • загар x = a; дитяче ліжечко x = a
   • Ви можете вирішити основні тригонометричні рівняння, вивчаючи різні положення кривої x на тригонометричному колі та використовуючи тригонометричну таблицю перетворень (або калькулятор). Щоб повністю зрозуміти, як розв’язувати ці та подібні основні тригонометричні рівняння, прочитайте наступну книгу: „Тригонометрія: Розв’язування тригонометричних рівнянь та нерівностей” (Електронна книга Amazon, 2010).
   • Приклад 1. Розв’язати за гріх x = 0,866. Таблиця перетворення (або калькулятор) дає відповідь: x = Pi / 3. Тригонометричне коло дає іншу криву (2Pi / 3) з однаковим значенням для синуса (0,866). Тригонометричне коло також забезпечує нескінченність відповідей, які називаються розширеними відповідями.
   • x1 = Pi / 3 + 2k.Pi та x2 = 2Pi / 3. (Відповіді протягом періоду (0, 2Pi))
   • x1 = Pi / 3 + 2k Pi та x2 = 2Pi / 3 + 2k Pi. (Детальні відповіді).
   • Приклад 2. Розв’яжіть: cos x = -1/2. Калькулятори дають x = 2 Pi / 3. Тригонометричне коло також дає x = -2Pi / 3.
   • x1 = 2Pi / 3 + 2k.Pi, а x2 = - 2Pi / 3. (Відповіді за період (0, 2Pi))
   • x1 = 2Pi / 3 + 2k Pi, і x2 = -2Pi / 3 + 2k.Pi. (Розширені відповіді)
   • Приклад 3. Розв’язати: tan (x - Pi / 4) = 0.
   • x = Pi / 4; (Відповідь)
   • x = Pi / 4 + k Pi; (Розширена відповідь)
   • Приклад 4. Розв’язати: ліжечко 2x = 1,732. Калькулятори та тригонометричне коло дають:
   • x = Pi / 12; (Відповідь)
   • x = Pi / 12 + k Pi; (Розширені відповіді)
3. Вивчіть перетворення, що використовуються при розв’язуванні тригонометричних рівнянь.
   • Для перетворення заданого тригонометричного рівняння у стандартні тригонометричні рівняння використовуйте стандартні алгебраїчні перетворення (розкладання на множники, спільний множник, поліноми ...), визначення та властивості тригонометричних функцій та тригонометричних тотожностей. Існує близько 31, 14 з яких є тригонометричними тотожностями, від 19 до 31, які також називаються тотожностями перетворення, оскільки вони використовуються при перетворенні тригонометричних рівнянь. Див. Вищезазначену книгу.
   • Приклад 5: Тригонометричне рівняння: sin x + sin 2x + sin 3x = 0 можна перетворити на добуток основних тригонометричних рівнянь, використовуючи тригонометричні тотожності: 4cos x * sin (3x / 2) * cos (x / 2) = 0. Основними тригонометричними рівняннями для розв’язання є: cos x = 0; гріх (3x / 2) = 0; і cos (x / 2) = 0.
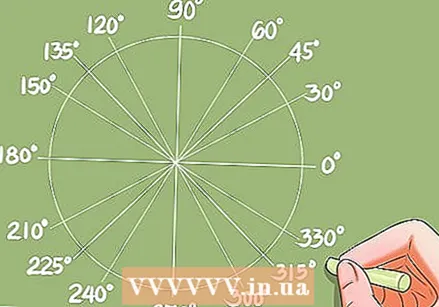4. Знайдіть криві, для яких відомі тригонометричні функції.
   • Перш ніж ви зможете навчитися розв’язувати тригонометричні рівняння, вам слід знати, як швидко знайти криві, для яких відомі тригонометричні функції. Значення перетворення кривих (або кутів) можна визначити за допомогою тригонометричних таблиць або калькулятора.
   • Приклад: Розв’язати для cos x = 0,732. Калькулятор дає рішення x = 42,95 градусів. Одиничне коло дає інші криві з однаковим значенням для косинуса.
5. Накресліть дугу відповіді на одиничному колі.
   • Ви можете створити графік для ілюстрації рішення на одиничному колі. Кінцевими точками цих кривих є правильні многокутники на тригонометричному колі. Кілька прикладів:
   • Кінцеві точки кривої x = Pi / 3 + k. Pi / 2 - це квадрат на одиничному колі.
   • Криві x = Pi / 4 + k.Pi / 3 представлені координатами шестикутника на одиничному колі.
6. Дізнайтеся, як розв’язувати тригонометричні рівняння.
   • Якщо дане тригонометричне рівняння містить лише одну тригонометричну функцію, розв’яжіть її як стандартне тригонометричне рівняння. Якщо дане рівняння містить дві або більше тригонометричних функцій, існує 2 методи рішення, залежно від варіантів перетворення рівняння.
     • А. Метод 1.
   • Перетворіть тригонометричне рівняння у добуток виду: f (x) .g (x) = 0 або f (x) .g (x) .h (x) = 0, де f (x), g (x) і h (x) - основні тригонометричні рівняння.
   • Приклад 6. Розв’язати: 2cos x + sin 2x = 0. (0 x 2Pi)
   • Рішення. Замініть sin 2x у рівнянні, використовуючи тотожність: sin 2x = 2 * sin x * cos x.
   • cos x + 2 * sin x * cos x = 2cos x * (sin x + 1) = 0. Тоді розв’яжіть 2 стандартні тригонометричні функції: cos x = 0 і (sin x + 1) = 0.
   • Приклад 7. Розв’язати: cos x + cos 2x + cos 3x = 0. (0 x 2Pi)
   • Рішення: Перетворіть це у виріб, використовуючи тригонометричні тотожності: cos 2x (2cos x + 1) = 0. Тепер розв’яжіть 2 основні тригонометричні рівняння: cos 2x = 0 та (2cos x + 1) = 0.
   • Приклад 8. Розв’язати: sin x - sin 3x = cos 2x. (0 x 2Pi)
   • Рішення: Перетворіть це у виріб, використовуючи тригонометричні тотожності: -cos 2x * (2sin x + 1) = 0. Тепер розв’яжіть 2 основні тригонометричні рівняння: cos 2x = 0 і (2sin x + 1) = 0.
     • B. Підхід 2.
   • Перетворює рівняння тригера на рівняння тригера лише з однією унікальною триго функцією як змінною. Є кілька порад щодо вибору відповідної змінної. Загальними змінними є: sin x = t; cos x = t; cos 2x = t, tan x = t і tan (x / 2) = t.
   • Приклад 9. Розв’яжіть: 3sin ^ 2 x - 2cos ^ 2 x = 4sin x + 7 (0 x 2Pi).
   • Рішення. У рівнянні замініть (cos ^ 2x) на (1 - sin ^ 2x) та спростіть рівняння:
   • 3sin ^ 2 x - 2 + 2sin ^ 2 x - 4sin x - 7 = 0. Тепер використовуйте sin x = t. Рівняння стає: 5t ^ 2 - 4t - 9 = 0. Це квадратне рівняння з 2 коренями: t1 = -1 і t2 = 9/5. Ми можемо відхилити другий t2, оскільки> 1. Тепер вирішимо для: t = sin = -1 -> x = 3Pi / 2.
   • Приклад 10. Розв’язати: tan x + 2 tan ^ 2 x = cot x + 2.
   • Рішення. Використовуйте tan x = t. Перетворіть подане рівняння у рівняння з t як змінну: (2t + 1) (t ^ 2 - 1) = 0. Вирішіть для t цей виріб, а потім розв’яжіть стандартне тригонометричне рівняння tan x = t для x.
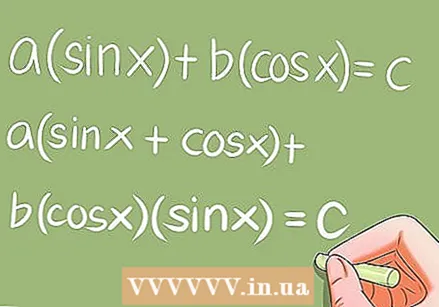7. Розв’яжіть спеціальні тригонометричні рівняння.
   • Існує кілька спеціальних тригонометричних рівнянь, які вимагають певних перетворень. Приклади:
   • a * sin x + b * cos x = c; a (sin x + cos x) + b * cos x * sin x = c;
   • a * sin ^ 2 x + b * sin x * cos x + c * cos ^ 2 x = 0
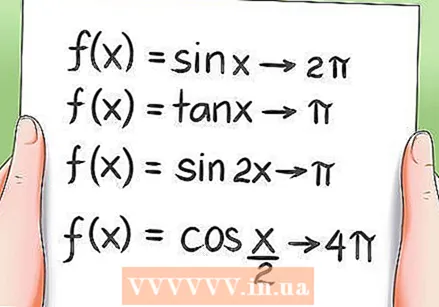8. Вивчити періодичні властивості тригонометричних функцій.
   • Усі тригонометричні функції є періодичними, що означає, що вони повертаються до одного і того ж значення після обертання протягом періоду. Приклади:
     • Функція f (x) = sin x має 2Pi як крапку.
     • Функція f (x) = tan x має Pi як крапку.
     • Функція f (x) = sin 2x має Pi як крапку.
     • Функція f (x) = cos (x / 2) має 4Pi як період.
   • Якщо період вказується у вправах / тесті, то вам просто потрібно знайти криву (и) x протягом цього періоду.
   • ПРИМІТКА. Розв’язування тригонометричних рівнянь складне і часто призводить до помилок та помилок. Тому відповіді слід ретельно перевіряти. Після розв’язання можна перевірити відповіді за допомогою графічного калькулятора для прямого подання даного тригонометричного рівняння R (x) = 0. Відповіді (як квадратний корінь) подаються в десяткових знаках. Як приклад, Pi має значення 3,14