Зміст

• кроки
• Метод 1 з 3: Частина 1: Визначення точки перегину
• Метод 2 з 3: Обчислення похідних функції
• Метод 3 з 3: Частина 3: Пошук точки перегину
• Поради

У диференціальному обчисленні точка перегину - ця точка кривої, в якій її кривизна змінює знак (з плюса на мінус або з мінуса на плюс). Це поняття використовується в машинобудуванні, економіці і статистиці для визначення істотних змін в даних.

кроки

Метод 1 з 3: Частина 1: Визначення точки перегину

1. 1 Визначення увігнутою функції. Середина будь хорди (відрізок, що з'єднує дві точки) графіка увігнутою функції лежить або під графіком, або на ньому.
2. 2 Визначення опуклої функції. Середина будь хорди (відрізок, що з'єднує дві точки) графіка опуклою функції лежить або над графіком, або на ньому.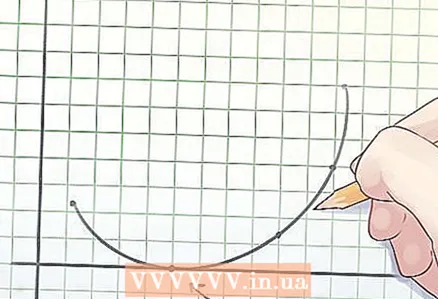
3. 3 Визначення коренів функції. Корінь функції - це таке значення змінної «х», при якому у = 0.
   • При побудові графіка функції коріння - це точки, в яких графік перетинає вісь Х.

Метод 2 з 3: Обчислення похідних функції

1. 1 Знайдіть першу похідну функції. Подивіться правила диференціювання в підручнику; ви повинні навчитися брати перші похідні, і тільки потім переходити до більш складних обчислень. Перші похідні позначаються як f '(х). Для виразів виду ax ^ p + bx ^ (p-1) + cx + d перша похідна має вигляд: apx ^ (p-1) + b (p - 1) x ^ (p-2) + c.
   • Наприклад, знайдіть точки перегину функції f (х) = х ^ 3 + 2х -1. Перша похідна цієї функції має вигляд:
     
     f '(x) = (x ^ 3 + 2x - 1)' = (x ^ 3) '+ (2x)' - (1) '= 3x ^ 2 + 2 + 0 = 3x2 + 2
2. 2 Знайдіть другу похідну функції. Друга похідна - це похідна від першої похідної вихідної функції. Друга похідна позначається як f '' (x).
   • У наведеному вище прикладі друга похідна має вигляд:
     
     f '' (x) = (3x2 + 2) '= 2 × 3 × x + 0 = 6x
3. 3 Прирівняти другу похідну до нуля і вирішите отримане рівняння. Отриманий результат буде передбачуваною точкою перегину.
   • У наведеному вище прикладі ваш розрахунок виглядає наступним чином:
     
     f '' (x) = 0
     6x = 0
     x = 0
4. 4 Знайдіть третю похідну функції. Щоб переконатися, що отриманий результат насправді є точкою перегину, знайдіть третю похідну, яка є похідною від другої похідної вихідної функції. Третя похідна позначається як f '' '(x).
   • У наведеному вище прикладі третя похідна має вигляд:
     
     f '' '(x) = (6x)' = 6

Метод 3 з 3: Частина 3: Пошук точки перегину

1. 1 Перевірте третю похідну. Стандартне правило оцінки передбачуваної точки перегину: якщо третя похідна не дорівнює нулю (тобто f '' '(x) ≠ 0), то передбачувана точка перегину є справжньою точкою перегину. Перевірте третю похідну; якщо вона не дорівнює нулю, то ви знайшли справжню точку перегину.
   • У наведеному вище прикладі третя похідна дорівнює 6, а не 0.Тому ви знайшли справжню точку перегину.
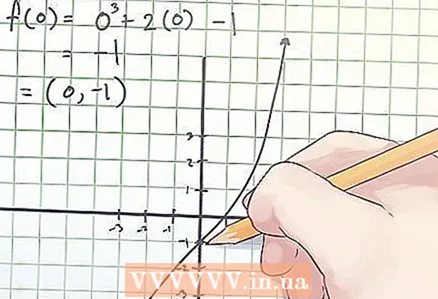2. 2 Знайдіть координати точки перегину. Координати точки перегину позначаються як (x, f (x)), де х - значення незалежної змінної «х» в точці перегину, f (х) - значення залежної змінної «у» в точці перегину.
   • У наведеному вище прикладі при прирівнювання другої похідної до нуля ви знайшли, що х = 0. Таким чином, щоб визначити координати точки перегину, знайдіть f (0). Ваш розрахунок виглядає наступним чином:
     
     f (0) = 0 ^ 3 + 2 × 0-1 = -1.
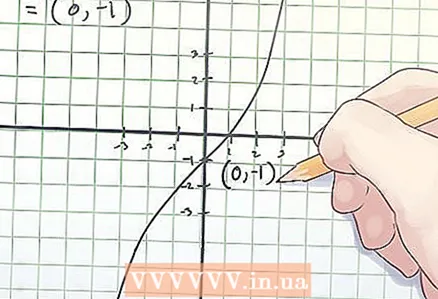3. 3 Запишіть координати точки перегину. Координати точки перегину - це знайдені значення «х» і f (x).
   • У наведеному вище прикладі точка перегину - це точка з координатами (0, -1).

Поради

• Перша похідна від вільного члена (простого числа) завжди дорівнює нулю.